カオス混合
水などの粘性の小さい流体では,流れを乱流化することが効率よく混合するための良い手段である. 一方,例えば,化学プラントなどで非常に粘性の大きい2つの液体を混合する場合には, 流れを乱流にすることは大きなパワーを必要とし,現実問題としては難しい. (例えば,大きな容器に入れた水あめのような流体を混合する場合を考えてほしい). そこで,容器や攪拌翼のゆっくりとした運動によって作り出される層流状態の速度場について, 効率が良くしかも一様な混合をいかにして達成するかという問題が生じる. これは,化学工学等の分野で古くから研究されてきたが, この種の問題をカオスを含む力学系の理論の立場から調べる研究が始まったのは比較的最近である.
いま,2つの流体の混合を考えることにして,初期の2流体の境界面上のすべての点に対して, その位置を初期値として流体粒子の運動を支配する方程式を解くと,境界面の時間発展が求まる. 2流体がすみやかに混合するためには,この境界面は小さい間隔で折りたたまれていく必要があるから, 境界面の面積は急激に増加しなければならず,最初ごく近くにいた境界面上の2点の間の距離は, 急速に増大する必要がある.この要請は,まさにカオス解のもっている性質(軌道不安定性)そのものである. 従って,大ざっぱにいうと,流体粒子がカオス的に振る舞うときには効率の良い混合が期待される. このような,流体粒子の運動がカオスとなり得るような速度場の下での混合は,しばしば「カオス混合」と呼ばれる.
乱流のように,速度場が時間的,空間的に不規則に変動している場合も,流体粒子は当然不規則に動く. しかし通常は,カオス混合という言葉は,時間的に一定あるいは時間の周期関数である比較的単純な速度場に対して用いられる.
参考文献:
[1] 船越満明,「カオス混合」,日本流体力学会誌ながれ,15巻,4号,(1996) pp.261-264.
[2] 船越満明, 金子 豊, "複雑系、カオスとシミュレーション", シミュレーション, 第19巻第4号, pp.282-289,2000.
[3] J.M.オッティーノ,「液体はどのように混ざり合うか」, サイエンス, 1989年3月号, 50-63ページ.
[4] "The Kinematics of Mixing : Stretching, Chaos, and Transport", by J.M.Ottino, Cambridge Univ. Press (1989).

(a)
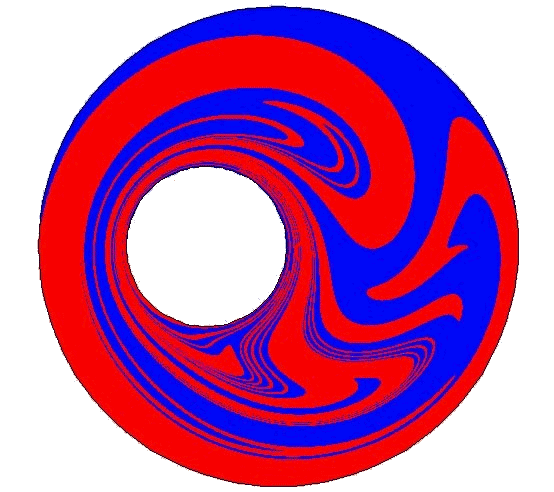
(b)
偏心二円筒の回転による,二円筒間の2つの流体の混合. (a) 混合前.(b) 混合後.
図(a)のように内円筒と外円筒の間にみたされている2つの流体を, これらの円筒をある角度ずつ交互にゆっくりと回転することによって混合させることを考える. このとき,2つの円筒の1回ごとの回転角度,内円筒と外円筒の位置関係をうまく選ぶと, 2つの流体のほとんどすべての部分はカオス運動をする.すなわち,流体の各微小部分は2円筒間の領域を不規則に動き回る. その場合には,カオスの特徴である初期値(今の場合は流体の各微小部分の初期位置)の差の指数関数的増大に対応して, 最初近くにあった流体どうしがどんどん離れていく.従って2つの流体の境界線も, 円筒の回転に伴って急激に引き延ばされていくと予想される. 一方,2流体の占める領域の大きさは有限であるので,このような引き延ばしが可能であるためには, この境界線は細かく折り畳まれていく必要がある.その結果,2つの流体は良く混合される. 図(b)は,流体のほとんどすべての部分がカオス運動を行うときの混合のようすで,外円筒を1回転, 内円筒を3回転という回転を2周期分行っただけでかなり良く混じっているのがわかる.
(注)図(b)の作成においては、
外円筒を半周期分(0.5回転)動かす→内円筒を1周期分(3回転)動かす→外円筒を半周期分(0.5回転)動かす
という操作を2回行った。